Back-Propagation-Neural-Network

本项目是对项目 GavinTechStudio/bpnn_with_cpp 的代码重构，基于C++实现基础BP神经网络，有助于深入理解BP神经网络原理。

项目结构

xxxxxxxxxx
.
├── CMakeLists.txt
├── data
│   ├── testdata.txt
│   └── traindata.txt
├── lib
│   ├── Config.h
│   ├── Net.cpp
│   ├── Net.h
│   ├── Utils.cpp
│   └── Utils.h
└── main.cpp

主要框架

• Net：网络具体实现

• Config：网络参数设置

• Utils：工具类

  • 数据加载
  • 激活函数

• main：网络具体应用

训练原理

具体公式推导请看视频讲解彻底搞懂BP神经网络 理论推导+代码实现（C++）

注意：本部分文档包含大量数学公式，由于GitHub markdown不支持数学公式渲染，推荐以下阅读方式：

1. 如果您使用的是Chrome、Edge、Firefox等浏览器，可以安装插件MathJax Plugin for Github（需要网络能够访问chrome web store）。
2. 使用PDF的方式进行阅读（推荐）。
3. 使用预渲染的静态网页进行阅读（推荐）。
4. 按.键或点击链接进入GitHub在线IDE预览README.md文件。

0. 神经网络结构图

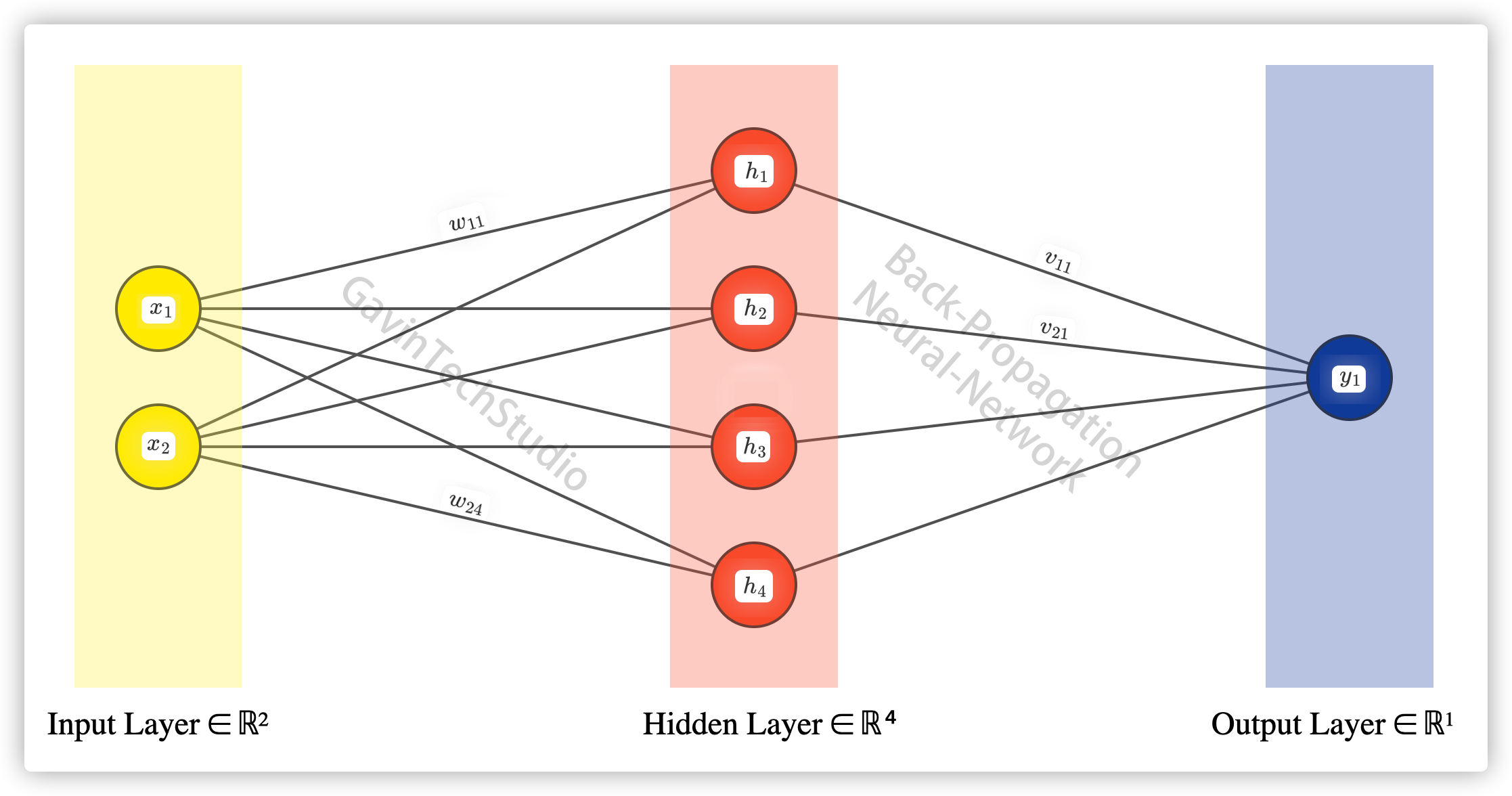
1. Forward（前向传播）

1.1 输入层向隐藏层传播

其中$h_j$$h_j$为第$j$$j$个隐藏层节点的值，$x_i$$x_i$为第$i$$i$个输入层节点的值，$w_{ij}$$w_{ij}$为第$i$$i$个输入层节点到第$j$$j$个隐藏层节点的权重，${\beta }_j$$\beta_j$为第$j$$j$个隐藏层节点偏置值，$\sigma (x)$$\sigma(x)$为Sigmoid激活函数，后续也将继续用这个表达，其表达式如下

本项目中的代码实现如下：

xxxxxxxxxx
for (size_t j = 0; j < Config::HIDENODE; ++j) {
    double sum = 0;
    for (size_t i = 0; i < Config::INNODE; ++i) {
        sum += inputLayer[i]->value * 
               inputLayer[i]->weight[j];
    }
    sum -= hiddenLayer[j]->bias;
  
    hiddenLayer[j]->value = Utils::sigmoid(sum);
}

1.2 隐藏层向输出层传播

其中$\widehat{y_k}$$\hat{y_k}$为第$k$$k$个输出层节点的值（预测值），$h_j$$h_j$为第$j$$j$个隐藏层节点的值，$v_{jk}$$v_{jk}$为第$j$$j$个隐藏层节点到第$k$$k$个输出层节点的权重，${\lambda }_k$$\lambda_k$为第$k$$k$个输出层节点的偏置值，$\sigma (x)$$\sigma(x)$为激活函数。

本项目中的代码实现如下：

xxxxxxxxxx
for (size_t k = 0; k < Config::OUTNODE; ++k) {
    double sum = 0;
    for (size_t j = 0; j < Config::HIDENODE; ++j) {
        sum += hiddenLayer[j]->value * 
               hiddenLayer[j]->weight[k];
    }
    sum -= outputLayer[k]->bias;
    
    outputLayer[k]->value = Utils::sigmoid(sum);
}

2. 计算损失函数（Loss Function）

损失函数定义如下：

其中$y_k$$y_k$为第$k$$k$个输出层节点的目标值（真实值），$\widehat{y_k}$$\hat{y_k}$为第$k$$k$个输出层节点的值（预测值）。

本项目中的代码实现如下：

xxxxxxxxxx
double loss = 0.f;

for (size_t k = 0; k < Config::OUTNODE; ++k) {
    double tmp = std::fabs(outputLayer[k]->value - label[k]);
    los += tmp * tmp / 2;
}

3. Backward（反向传播）

利用梯度下降法进行优化。

3.1 计算$\mathrm{\Delta }{\lambda }_k$$\Delta \lambda_k$（输出层节点偏置值的修正值）

其计算公式如下（激活函数为Sigmoid时）：

其中$\eta$$\eta$为学习率（其余变量上方已出现过不再进行标注）。

本项目中的代码实现如下：

xxxxxxxxxx
for (size_t k = 0; k < Config::OUTNODE; ++k) {
    double bias_delta = 
        -(label[k] - outputLayer[k]->value) *
        outputLayer[k]->value *
        (1.0 - outputLayer[k]->value);
    
    outputLayer[k]->bias_delta += bias_delta;
}

3.2 计算$\mathrm{\Delta }{v}_{jk}$$\Delta v_{jk}$（隐藏层节点到输出层节点权重的修正值）

其计算公式如下（激活函数为Sigmoid时）：

其中$h_j$$h_j$为第$j$$j$个隐藏层节点的值（其余变量上方已出现过不再进行标注）。

本项目中的代码实现如下：

xxxxxxxxxx
for (size_t j = 0; j < Config::HIDENODE; ++j) {
    for (size_t k = 0; k < Config::OUTNODE; ++k) {
        double weight_delta =
            (label[k] - outputLayer[k]->value) * 
            outputLayer[k]->value * 
            (1.0 - outputLayer[k]->value) * 
            hiddenLayer[j]->value;

        hiddenLayer[j]->weight_delta[k] += weight_delta;
    }
}

3.3 计算$\mathrm{\Delta }{\beta }_j$$\Delta \beta_j$（隐藏层节点偏置值的修正值）

其计算公式如下（激活函数为Sigmoid时）：

其中$v_{jk}$$v_{jk}$为第$j$$j$个隐藏层节点到第$k$$k$个输出层节点的权重（其余变量上方已出现过不再进行标注）。

本项目中的代码实现如下：

xxxxxxxxxx
for (size_t j = 0; j < Config::HIDENODE; ++j) {
    double bias_delta = 0.f;
    for (size_t k = 0; k < Config::OUTNODE; ++k) {
        bias_delta += 
            -(label[k] - outputLayer[k]->value) * 
            outputLayer[k]->value * 
            (1.0 - outputLayer[k]->value) * 
            hiddenLayer[j]->weight[k];
    }
    bias_delta *= 
        hiddenLayer[j]->value * 
        (1.0 - hiddenLayer[j]->value);

    hiddenLayer[j]->bias_delta += bias_delta;
}

3.4 计算$\mathrm{\Delta }{w}_{ij}$$\Delta w_{ij}$（输入层节点到隐藏层节点权重的修正值）

其计算公式如下（激活函数为Sigmoid时）：

其中$x_i$$x_i$为第$i$$i$个输入层节点的值（其余变量上方已出现过不再进行标注）。

本项目中的代码实现如下：

xxxxxxxxxx
for (size_t i = 0; i < Config::INNODE; ++i) {
    for (size_t j = 0; j < Config::HIDENODE; ++j) {
        double weight_delta = 0.f;
        for (size_t k = 0; k < Config::OUTNODE; ++k) {
            weight_delta +=
                (label[k] - outputLayer[k]->value) * 
                outputLayer[k]->value * 
                (1.0 - outputLayer[k]->value) * 
                hiddenLayer[j]->weight[k];
        }
        weight_delta *=
            hiddenLayer[j]->value * 
            (1.0 - hiddenLayer[j]->value) * 
            inputLayer[i]->value;

        inputLayer[i]->weight_delta[j] += weight_delta;
    }
}